CARTESIO E NEWTON
 Nel XVII secolo in corrispondenza alle trasformazioni
economico-politiche, anche la cultura subisce profondi
cambiamenti. Il processo di laicizzazione, già iniziato nel rinascimento (D) si accelera e
si approfondisce dando luogo ad un profondo interesse per la natura (D). Gli studiosi tentano di
delineare ambiziosi sistemi generali da sostituire a quelli che
avevano costituito la base della vecchia cultura. Il più urgente
problema dei pensatori del Seicento sarà di scoprire una
giustificazione metafisica (D) alla comune
fiducia nella ragione, in questo secolo "la lotta per la
ragione" si può dire essere il segno della cultura
filosofica, infatti questa lotta fa prevalere la ragione e
l’autonomia di giudizio, nel dominio morale, politico e
religioso. Il nostro intelletto vuole intuire i principi
dell’unità del mondo, quindi il vero filosofo è ritenuto
chi contribuisce in modo effettivo alla scoperta di questi
principi; non importa se lo si preferisca qualificare come fisico
o come matematico o come metafisico. Così vengono qualificati
filosofi tanto Cartesio (SB) quanto Newton (SB)che svolgono le loro
attività filosofiche, fisiche, matematiche, l’uno nella
prima metà del secolo XVII e l’altro alla fine.
Nel XVII secolo in corrispondenza alle trasformazioni
economico-politiche, anche la cultura subisce profondi
cambiamenti. Il processo di laicizzazione, già iniziato nel rinascimento (D) si accelera e
si approfondisce dando luogo ad un profondo interesse per la natura (D). Gli studiosi tentano di
delineare ambiziosi sistemi generali da sostituire a quelli che
avevano costituito la base della vecchia cultura. Il più urgente
problema dei pensatori del Seicento sarà di scoprire una
giustificazione metafisica (D) alla comune
fiducia nella ragione, in questo secolo "la lotta per la
ragione" si può dire essere il segno della cultura
filosofica, infatti questa lotta fa prevalere la ragione e
l’autonomia di giudizio, nel dominio morale, politico e
religioso. Il nostro intelletto vuole intuire i principi
dell’unità del mondo, quindi il vero filosofo è ritenuto
chi contribuisce in modo effettivo alla scoperta di questi
principi; non importa se lo si preferisca qualificare come fisico
o come matematico o come metafisico. Così vengono qualificati
filosofi tanto Cartesio (SB) quanto Newton (SB)che svolgono le loro
attività filosofiche, fisiche, matematiche, l’uno nella
prima metà del secolo XVII e l’altro alla fine.
Il periodo che intercorre tra Cartesio e
Newton, che vede in attività studiosi come Spinoza (SB), Pascal (SB), Hobbes (SB), è
caratterizzato da un fiorire di ricerche sperimentali e di studi
teorici, in cui i legami della matematica con la fisica si
intensificano. Il binomio galileiano delle "necessarie dimostrazioni e sensate esperienze", che costituisce il fondamento della nuova
fisica, presuppone l’impiego di più efficienti strumenti,
ed è proprio nel ‘600 che la strumentazione scientifica si arricchisce e si perfeziona.
Cartesio si pone come obbiettivo quello di
conseguire la saggezza e la scienza di tutto ciò che riesce
utile all’uomo, per questo elabora un metodo, cioè un
procedimento ordinato di indagine composto da una serie di regole
atte ad evitare l’errore e a raggiungere risultati validi
per il dominio dell’uomo sulla natura. Il metodo si articola
in quattro regole: l’evidenza, che è la più importante,
l’analisi, la sintesi e l’enumerazione, detta anche
revisione.
Secondo Cartesio per trovare il fondamento di
un metodo che deve essere la guida della ricerca in tutte le
scienze è possibile solamente attraverso una critica radicale di
tutto il sapere già dato. Da qui il "dubbio metodico";
tale strumento si propone di approdare a delle conoscenze
indubitabili attraverso l’esercizio del dubbio (vedi pensiero
filosofico di Cartesio).
Egli avvalorò l’impostazione meccanicistica (D) della scienza
con la separazione tra soggetto e oggetto, e il conseguente
dualismo tra materia (res extensa) e pensiero (res cogitans),che
risolse ricorrendo all’ipotesi della ghiandola Pineale. La
"Geometria" costituisce la più importante delle tre
appendici del "Discorso sul Metodo" e dà i natali alla
geometria analitica, che si colloca come punto di incontro fra la
geometria degli antichi e l’algebra dei moderni. Cartesio ha
consapevolezza dell’unità delle diverse scienze
matematiche, che pur operando su oggetti differenti, considerano
soltanto i diversi rapporti e proporzioni. Renè Descartes
riordina sistematicamente la simbologia algebrica e accoglie
l’immediata interpretazione geometrica dei procedimenti
algebrici. Applica il suo metodo alla geometria degli antichi,
quasi tutti "colpevoli" di procedere episodicamente,
senza sollevarsi al livello di generalità necessaria ad
un’impostazione sistematica della scienza. L’algebra
diviene idonea a riprodurre entro di sé in termini formali la
geometria, la quale a sua volta si offre come strumento di
chiarificazione dei procedimenti algebrici. Il numero e la forma
divengono traducibili l’uno nell’altro.
Cartesio introduce l’uso sistematico degli
assi coordinati, che oggi vengono detti "assi
cartesiani", che permettono di rappresentare i punti con
coppie o terne di numeri e le relazioni geometriche fra i punti
con relazioni algebriche. Il metodo cartesiano ha una preistoria,
infatti l’individuazione di ciascun punto su di una
superficie attraverso una coppia ordinata di numeri (la
latitudine e la longitudine) era già una pratica usata nella
cartografia, alla quale risale anche l’individuazione di una
linea mediante una sola coordinata (la sola latitudine individua
un parallelo e la sola longitudine un meridiano). Generalizzando
il principio , Cartesio afferma che una equazione a due incognite
individua sempre una linea, che è una retta se l’equazione
è di primo grado (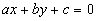 ); è una conica se l’equazione è di
secondo grado (ad esempio una circonferenza
); è una conica se l’equazione è di
secondo grado (ad esempio una circonferenza 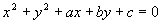 , o una parabola
, o una parabola 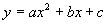 , o una iperbole
, o una iperbole 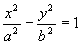 , o un ellisse
, o un ellisse 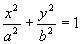 ); ed è infine una curva più complessa
se l’equazione è di grado superiore(
); ed è infine una curva più complessa
se l’equazione è di grado superiore( 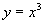 ).
).
Fra i risultati più importanti ottenuti da
Cartesio, merita una particolare menzione la determinazione
generale della normale a una qualsiasi curva algebrica piana in
un suo punto qualunque e la conseguente determinazione della
tangente.
Il mondo si identifica con l’estensione e
perciò la fisica si riconduce integralmente alla geometria, né
è di ostacolo a tale riduzione l’estensione del moto,
giacchè il tempo può assumere agevolmente i connotati di una
dimensione geometrica, come si vede nel seguente grafico.
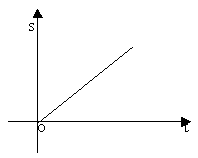 (diagramma orario)
(diagramma orario)
Nelle opere di fisica di Cartesio c’è
un’assenza quasi totale della matematica, infatti a lui
interessa fornire della realtà fisica un’interpretazione
matematica, senza che con questo si senta obbligato a svolgerla
esplicitamente. La fisica cartesiana si basa essenzialmente su
due principi: (1)Inesistenza del vuoto ;(2)Costanza della
quantità di moto.
La negazione dell’esistenza del vuoto è
una diretta conseguenza dell’estensione come attributo della
sostanza corporea, da ciò, essendo l’estensione un
attributo e non una sostanza non può esistere di per sè senza
appoggiarsi a qualche corpo. Cartesio per questo deduce
l’esistenza di una materia prima entro la quale i corpi si
muoverebbero come pietre nell’acqua. Nella fisica cartesiana
tutti i fenomeni si spiegano per mezzo del movimento, questo
sarebbe caratterizzato dalla "quantità di moto", ossia
dal prodotto della massa del corpo in movimento per la sua
velocità (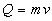 ). Egli assolutizza questo
principio, mentre oggi sappiamo che è valido quando e solo
quando venga applicato ad un sistema di masse soggette unicamente
alle forze che esercitano l’una sull’altra, ovvero ad
un sistema isolato.
). Egli assolutizza questo
principio, mentre oggi sappiamo che è valido quando e solo
quando venga applicato ad un sistema di masse soggette unicamente
alle forze che esercitano l’una sull’altra, ovvero ad
un sistema isolato.
Il "grande errore di Cartesio" fu
quello di considerare l’originaria quantità di moto, che
può distribuirsi in modi differenti tra i corpi attraverso gli
urti, come l’unico motore della grande macchina del mondo.
Egli bandiva ogni tipo di forza, attrattiva o repulsiva; secondo
Cartesio ciò che si mantiene è la quantità di moto (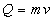 ), mentre in realtà si mantiene
l’energia (
), mentre in realtà si mantiene
l’energia (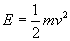 ), che può trasformarsi nelle sue varie
forme: cinetica, termica, ecc. Su questo aspetto della fisica
cartesiana punterà verrà in contraddizione Leibniz (vedi relazione
Leibniz).
), che può trasformarsi nelle sue varie
forme: cinetica, termica, ecc. Su questo aspetto della fisica
cartesiana punterà verrà in contraddizione Leibniz (vedi relazione
Leibniz).
Egli ammette il principio di inerzia sia come
conservazione della velocità iniziale, sia come conservazione
della direzione rettilinea del moto. Partendo dai principi sopra
accennati Cartesio formula la sua famosa "teoria dei
vortici", in cui diceva che una ogni corpo è attirato verso
la Terra da un vortice e analogamente i pianeti, inclusa la
Terra, ruotano in un vortice più grande attorno al Sole.
Con Newton l’unità di matematica e
fisica, scandagliata da Galileo, astrattamente formulata da
Cartesio e attiva nelle ricerche di molti studiosi del ‘600,
trova completa attenzione in un modello organico e unitario.
Newton tende a realizzare una scienza puramente
descrittiva dei fenomeni naturali e delle sue leggi. Con la sua
affermazione "hypotheses non fingo" voleva dire che la
scienza deve evitare qualsiasi ipotesi metafisica, intendendo
quelle ipotesi che ammettono qualità occulte o forze nascoste o
comunque fattori che sfuggono all’osservazione scientifica e
al calcolo matematico.
 Nei
"Principi", una delle maggiori opere scritte da Newton,
egli enuncia quattro regole fondamentali: (1)Bisogna ammettere
solo quelle cause che sono necessartie per spiegare i fenomeni
(questa regola ha un richiamo con il principio di
"economia" di Ockham (SB), il così detto
"rasoio", secondo cui è dannoso e inutile moltiplicare
gli enti: "Entes non sunt moltiplicandi praeter
necessitatem); (2)Effetti dello stesso genere devono essere
sempre attribuiti, finchè è possibile, alla stessa causa; (3)Le
qualità che non sono suscettibili di aumento e di diminuzione e
che appartengono a tutti i corpi dei quali si può fare
esperienza, devono essere considerate come appartenenti a tutti i
corpi in generale (deduzione); (4)Nella
filosofia sperimentale, le proposizioni raggiunte mediante
induzione dei fenomeni devono essere considerate vere fino al
momento in cui altri fenomeni le confermino errate o dimostrino
che sono soggette a eccezioni.
Nei
"Principi", una delle maggiori opere scritte da Newton,
egli enuncia quattro regole fondamentali: (1)Bisogna ammettere
solo quelle cause che sono necessartie per spiegare i fenomeni
(questa regola ha un richiamo con il principio di
"economia" di Ockham (SB), il così detto
"rasoio", secondo cui è dannoso e inutile moltiplicare
gli enti: "Entes non sunt moltiplicandi praeter
necessitatem); (2)Effetti dello stesso genere devono essere
sempre attribuiti, finchè è possibile, alla stessa causa; (3)Le
qualità che non sono suscettibili di aumento e di diminuzione e
che appartengono a tutti i corpi dei quali si può fare
esperienza, devono essere considerate come appartenenti a tutti i
corpi in generale (deduzione); (4)Nella
filosofia sperimentale, le proposizioni raggiunte mediante
induzione dei fenomeni devono essere considerate vere fino al
momento in cui altri fenomeni le confermino errate o dimostrino
che sono soggette a eccezioni.
Newton diede un contributo importante alla
matematica, soprattutto con l’invenzione del calcolo
infinitesimale, per il quale ideò due sistemazioni: il così
detto calcolo delle flussioni, che è quello più importante, e
quello delle prime e ultime ragioni.
Per il calcolo delle flussioni Newton partiva
dalla seguente constatazione: "le linee vengono descritte
per moto continuo dei punti, le superfici per moto di linee, i
solidi per moto di superfici, ecc.". I problemi del moto si
traducono in calcolo delle derivate e calcolo degli integrali.
Egli dette al suo metodo il nome di "flussione" per
indicare che si trattava di quantità variabili e della loro velocità (D) di
"flusso". Le nozioni base del calcolo differenziale e
integrale sono quelle di variabile e limite (ST). Le prime due sono
facilmente comprensibili, mentre l’ultima ha richiesto tempo
per essere chiarita. In matematica si intende per limite il
valore che tende ad assumere una funzione, quando la variabile
indipendente tende verso determinato valore (vedi Analisi
infinitesimale: Newton e Leibniz).
Per Newton il tempo e lo spazio essendo
assoluti preesistono ad ogni possibile percezione degli oggetti
in movimento; lo spazio è un contenitore infinitamente grande e
precede la creazione del mondo oggettivo, mentre il tempo scorre
in modo uniforme, sommando continuamente istanti infinitesimi
dall’origine della creazione ad un tempo infinito. Tempo e
spazio possono essere numerati da zero ad infinito come somme di
infinitesimi. Newton con questo metodo rese possibile il calcolo
delle velocità e delle accelerazioni istantanee
( 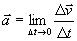 ;
; 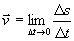 ).
).
Il
concetto il moto assoluto e di conseguenza quello di spazio e
tempo assoluto è essenziale per la meccanica di Newton, nei
"Principi", dove definisce i concetti base della fisica
e i tre principi della dinamica. Il risultato più importante da
lui raggiunto fu la legge della gravitazione universale ( 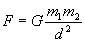 ), che regola i moti dei corpi celesti e
quelli dei corpi che cadono naturalmente sulla terra.
), che regola i moti dei corpi celesti e
quelli dei corpi che cadono naturalmente sulla terra.
Relatore:
Marco Cascianini
 Nel XVII secolo in corrispondenza alle trasformazioni
economico-politiche, anche la cultura subisce profondi
cambiamenti. Il processo di laicizzazione, già iniziato nel rinascimento (D) si accelera e
si approfondisce dando luogo ad un profondo interesse per la natura (D). Gli studiosi tentano di
delineare ambiziosi sistemi generali da sostituire a quelli che
avevano costituito la base della vecchia cultura. Il più urgente
problema dei pensatori del Seicento sarà di scoprire una
giustificazione metafisica (D) alla comune
fiducia nella ragione, in questo secolo "la lotta per la
ragione" si può dire essere il segno della cultura
filosofica, infatti questa lotta fa prevalere la ragione e
l’autonomia di giudizio, nel dominio morale, politico e
religioso. Il nostro intelletto vuole intuire i principi
dell’unità del mondo, quindi il vero filosofo è ritenuto
chi contribuisce in modo effettivo alla scoperta di questi
principi; non importa se lo si preferisca qualificare come fisico
o come matematico o come metafisico. Così vengono qualificati
filosofi tanto Cartesio (SB) quanto Newton (SB)che svolgono le loro
attività filosofiche, fisiche, matematiche, l’uno nella
prima metà del secolo XVII e l’altro alla fine.
Nel XVII secolo in corrispondenza alle trasformazioni
economico-politiche, anche la cultura subisce profondi
cambiamenti. Il processo di laicizzazione, già iniziato nel rinascimento (D) si accelera e
si approfondisce dando luogo ad un profondo interesse per la natura (D). Gli studiosi tentano di
delineare ambiziosi sistemi generali da sostituire a quelli che
avevano costituito la base della vecchia cultura. Il più urgente
problema dei pensatori del Seicento sarà di scoprire una
giustificazione metafisica (D) alla comune
fiducia nella ragione, in questo secolo "la lotta per la
ragione" si può dire essere il segno della cultura
filosofica, infatti questa lotta fa prevalere la ragione e
l’autonomia di giudizio, nel dominio morale, politico e
religioso. Il nostro intelletto vuole intuire i principi
dell’unità del mondo, quindi il vero filosofo è ritenuto
chi contribuisce in modo effettivo alla scoperta di questi
principi; non importa se lo si preferisca qualificare come fisico
o come matematico o come metafisico. Così vengono qualificati
filosofi tanto Cartesio (SB) quanto Newton (SB)che svolgono le loro
attività filosofiche, fisiche, matematiche, l’uno nella
prima metà del secolo XVII e l’altro alla fine.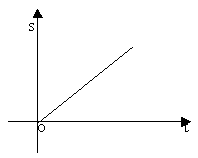 (diagramma orario)
(diagramma orario)