ANALISI INFINITESIMALE: NEWTON E LEIBNIZ

Questa relazione è stata ripresa dalla "Guida multimediale alla storia della civiltà europea diretta da Umberto Eco" e rivista in base alle conoscenze di una quarta classe del Liceo Scientifico.

"Uno dei grandi capitoli della ricerca matematica seicentesca è lo sviluppo dell’analisi infinitesimale, cui Newton (SB) e Leibniz (SB) forniscono i contributi decisivi. Essa si basa su due operazioni fondamentali, l’una inversa dell’altra: la "derivazione", connessa alla determinazione delle tangenti e alla ricerca dei massimi e minimi di una funzione e l’"integrazione", connessa al calcolo di aree (quadrature) e volumi (cubature).

Derivazione: tangenti, massimi e minimi

Le operazioni di derivazione nascono dal tentativo di mettere a punto una strategia di calcolo necessaria a risolvere problemi squisitamente scientifici, come, ad esempio, quello di trovare la velocità istantanea di un corpo in movimento conoscendo la sua legge di moto. Anche il problema delle tangenti, anticamente concepito come un problema essenzialmente geometrico, acquista, nel Seicento, una certa rilevanza dal punto di vista fisico, poiché la direzione di moto di un corpo in un determinato punto della sua traiettoria coincide con la direzione della tangente alla traiettoria nel punto dato. Infine, anche i problemi di massimo e di minimo scaturivano dallo studio delle traiettorie dei proiettili, e soprattutto dalla necessità di stabilire quali altezze massime avrebbero raggiunto se lanciate in aria con angoli di volta in volta differenti (un problema di grande interesse anche per gli ingegneri militari).

Integrazione: calcolo di aree e volumi

Il problema del calcolo di aree e volumi costituisce l’altro versante su cui si esercitano le menti dei matematici del Seicento. Il problema delle quadrature e delle cubature non è un settore nuovo della ricerca matematica, affondando le sue radici sin nell’antichità classica.

Tuttavia, nel corso del Seicento vengono sperimentati nuovi metodi, nuove strategie per conseguire non solo gli stessi risultati già trovati dai matematici della Grecia antica, ma anche per raggiungerne di nuovi.

Newton e Leibniz

Non è possibile spiegare la forma assunta, in Newton, dal calcolo infinitesimale senza accennare agli sviluppi delle funzioni in serie di potenze. Queste ricerche fornirono a Newton gli algoritmi (D) fondamentali con i quali sviluppa il suo calcolo. Newton raccoglie i risultati che, su questo argomento, erano stati ottenuti dalla scuola matematica inglese (Wallis, Gregory, Barrow), i quali avevano posto in luce l’importanza delle serie di potenze. Tuttavia egli riesce a raggiungere un risultato incomparabilmente più generale e più fecondo di quelli conseguiti dai suoi predecessori. Questo risultato è costituito dal "teorema del binomio", cioè dalla formula che estende lo sviluppo del binomio dal caso noto di r interoal caso allora ignoto di r qualunque, positivo o negativo, intero o frazionario. La serie che fornisce tale sviluppo è la nota serie di Newton:

E’ grazie a questo strumento che Newton può sviluppare, tra il 1665 e il 1666, i primi elementi fondamentali del suo calcolo, come poi dichiarerà in due lettere inviate nel 1676 a Oldenburg con l’incarico di comunicarle a Leibniz. Ma vediamone le applicazioni negli scritti che Newton dedica al calcolo, che mostrano, tra l’altro, nel loro sviluppo cronologico, le tappe con le quali Newton viene precisando gli elementi fondamentali della sua analisi. Nell’Analisi mediante equazioni con un numero infinito di termini, Newton, dopo aver trattato delle serie di potenze e di alcune operazioni su di esse, espone gli elementi fondamentali del suo calcolo infinitesimale, mostrando la relazione inversa tra derivazione e integrazione, punto centrale della moderna analisi.

Egli suppone di avere una curva come quella indicata in figura e che l’area sottostante sia data da: (1)

Newton considera poi un incremento infinitesimo di x, che chiama "momento" di x, denotandolo con x+.

L’area delimitata dalla curva, dall’asse x, dall’asse y e dall’ordinata corrispondente all’ascissa x+ viene denotata con z+y, dove y è l’incremento infinitesimo o "momento" dell’area.

Per cui la (1) diventa: . Elevando al quadrato per eliminare la radice al secondo membro si ottiene:

essendo si fa

sviluppando i calcoli e dividendo per

se è infinitamente piccolo, come assume Newton, allora i termini in si annullano e perciò si ha

Tenendo conto della (1) si ottiene alla fine l’ordinata: y = x½.

Così, nel linguaggio attuale, il tasso di variazione dell’area per ogni valore di x è uguale al valore della y del punto della curva corrispondente.

Viceversa, Newton dimostra che se la curva è data dall’equazione: allora l’area sottostante alla curva è:.

In un secondo lavoro di poco successivo al Metodo delle flussioni e delle serie infinite, Newton esplicita un diverso approccio ai problemi dell’analisi infinitesimale, che potremmo definire di tipo "cinematico" (D). Le grandezze geometriche sono ora concepite come generate da moti continui, anziché come aggregati di termini infinitesimi. Così, la curva dell’esempio precedente risulta generata dal moto continuo di un punto. Essendo dunque la curva una quantità variabile, Newton la chiama "fluente", mentre definisce "flussione" il suo tasso di variazione. Egli introduce anche una nuova notazione per indicare la flussione di una fluente x, denotandola con .

Il problema fondamentale del calcolo infinitesimale viene quindi impostato nei seguenti termini: data una relazione tra due fluenti x e y, trovare la relazione tra le rispettive flussioni e e viceversa. Le due variabili di cui è data la relazione possono rappresentare quantità qualsiasi. Tuttavia, Newton preferisce pensare ad esse (pur non ritenendolo, giustamente, necessario) come a grandezze variabili nel tempo.

Gottfried Wilhelm Leibniz scopre il suo calcolo, in tutto simile a quello di Newton, tra il 1673 e il 1676, a Parigi. Come egli stesso racconta, è determinante un lavoro di Pascal dedicato alla cicloide (D) dal titolo Trattato sui seni (D) di un quadrante di cerchio (1658) in cui compare il cosiddetto "triangolo caratteristico". (Animazione cicloide 20 KB)

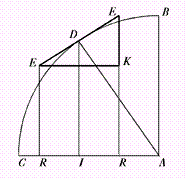
Pascal se ne era servito per la quadratura della funzione seno (D) (ma la figura ricorre, sotto varie forme, anche negli scritti di Torricelli (SB), Fermat (SB) e Barrow (SB): quest’ultimo se ne era servito, invece, per tracciare la tangente alla curva). Leibniz si rende conto che la determinazione della tangente alla curva dipende dal rapporto tra le differenze nelle ordinate e nelle ascisse quando queste divengono infinitamente piccole e che, viceversa, la quadratura, cioè il calcolo dell’area, dipende dalla somma delle ordinate moltiplicate per tratti infinitesimi di ascissa, ovvero dalle aree di rettangoli infinitamente sottili. Le operazioni di somma e di differenza sono in un rapporto inverso, perciò anche la quadratura e la determinazione della tangente stanno in un rapporto inverso. Questa scoperta del rapporto inverso tra le due operazioni ha in Leibniz la stessa rilevanza che abbiamo visto avere in Newton. In possesso dunque di un metodo di grandissima importanza, Leibniz deve elaborare un linguaggio e una notazione confacenti a questa nuova branca della matematica. Nella sua prima pubblicazione sul calcolo differenziale e integrale, il Nuovo metodo sui massimi e sui minimi e sulle tangenti, Leibniz mostra di essere in possesso della notazione differenziale divenuta poi classica. Egli parte da una curva y = f (x) e suppone che sia tracciata la tangente uscente da un punto (x, y) della curva. Dato poi a x un incremento qualsiasi che egli chiama "differenza" (e noi "differenziale") che indica con dx , sceglie quindi il differenziale della funzione, dy, in modo che il rapporto dy/dx uguagli il coefficiente direttivo della tangente (ossia la derivata). Dà, inoltre, le più importanti regole della differenziazione.

Nella Geometria nascosta il segno d’integrale appare nella forma attuale: che ricorda che un’area è la somma di rettangoli infinitesimi: il simbolo è l’ingrandimento della lettera s che indica, appunto, la somma.

Questa notazione è decisamente più efficace di quelle usate in precedenza. In un primo tempo, infatti, Leibniz aveva scritto omn. y (ossia, "tutte le y") e più tardi, prima della notazione definitiva del 1684, Leibniz scrive: che però indica la somma delle ordinate, ma questo sarebbe stato corretto per gli indivisibili cavalieriani, intesi come linee, anziché come aree.

Per concludere queste note su Newton e Leibniz è opportuno ricordare la durissima polemica che si accende tra i due circa la priorità della scoperta dell’analisi infinitesimale. In realtà la vera questione che verrà dibattuta è se Leibniz sia giunto da solo alla scoperta dell’analisi infinitesimale o se, invece, non abbia avuto notizia delle ricerche newtoniane durante il soggiorno londinese del 1673 e da queste abbia tratto gli spunti necessari per sviluppare la sua analisi. Leibniz respinge (e a ragione) le accuse di plagio e non mette mai in discussione il fatto che Newton sia giunto prima all’invenzione dell’analisi infinitesimale. Ma rivendicherà sempre l’autonomia delle proprie ricerche. La polemica è durissima e si protrae anche dopo la morte di Leibniz con il risultato di interrompere, per diversi decenni, lo scambio scientifico tra la scuola matematica inglese e quella continentale (la prima filo-newtoniana e la seconda filo-leibniziana)".